All the while I wanted to know the exact number of the cogs / cusps / scallops / teeth surrounding the Chartres labyrinth.
As well I noticed quite different values in some new built replicas of the Chartres labyrinth.
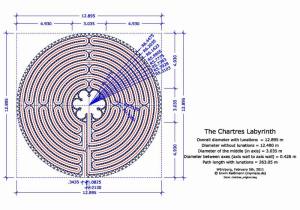
If there is no unequivocal opinion about sense and purpose of the same, at least the exact number of these elements should be clear. This is important for everybody which wants to copy an original Chartres labyrinth and at the same time a sign how exactly they have looked at the original. Finally, we can admire the original more than 800 years in the Cathedral Notre Dame of Chartres in France.
Graphic of the labyrinth
The information in the literature about the exact number is not so unequivocal as one could mean. It is the speech of 112 or 113. However, it seems to be clear that round a closed labyrinth 114 elements would exist and that one element was left out to form the entrance. By no means two elements would be necessary for that, because one fits perfectly. Therefore we get 113 lunations. Exact counting on good graphics or photos also amounts to 113.
One have speculated a lot why these are just 113 or 114 elements. The centre of the labyrinth exists of 6 “petals” which are open to the middle. The 6, multiplied by 19 (number of perfection, the sun, the flower of the life) results in 114 similarly constructed “rays” for the border of the labyrinth. The sum of the digits 114 is 6, like the number of the elements in the middle.
Photo of the entrance
Graphic of the entrance
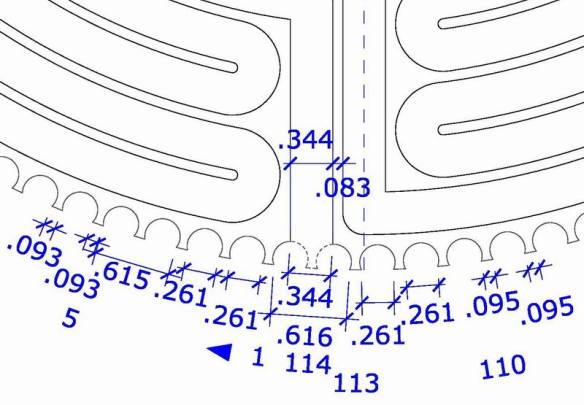
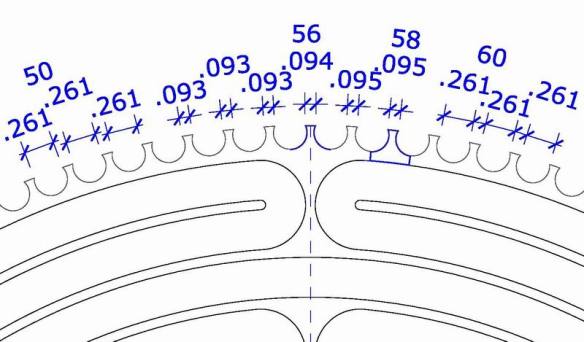
Only, how should one count, actually? The lunations around the labyrinth are made of circular parts which like gear wheels are built of jags and bowl-shaped deepening which are cut off in the upper part. I propose to call a gear wheel with a quarter circle on both sides as one element. Single components in the labyrinth are constructed like this, as the joints in the photos show (e.g., element 58 middle part at top).
The blue drawn unity should be counted as one element. If one applies this to the complete labyrinth, 114 elements arise in the closed labyrinth. If one cuts out one for the entrance, we have 113 remaining elements.
One could also count the “bowls” instead of the “peaks”. Then we would have 112 complete and two half parts (at the entrance). However, all together we would have again 113 items.
Photo of the middle part at top
Graphic of the middle part at top
Something else has struck me when I constructed the periphery of the lunations. The circumference of 40.511 m (given by a mean value for the diameter of 12.895 m) can be divided in 114 equal parts, this would be 0.355 m for each. The position of every single element should thereby result from that. If one begins with the division in the middle of the omitting element for the entrance (114 in the graphic), then the tooth on top (56 in the graphic) would not lie on the middle axis as it is the case quite obviously in the original.
The exact place of this part would be about 7 cm farther on the right. If one liked to keep up the exact number of the teeth, one must diminish the distances in the left half (element 1 – 56) and increase it in the right half(element 56 – 113). I do not know how the master builders of the Middle Ages handled this. Maybe they had quite different points of view?
Finally once again the statement: The Chartres labyrinth has 113 visible lunations.
Related post
Related Links
blogmymaze 