The 42 Alternating Labyrinths with One Axis and 7 Circuits

Question

As shown by Tony Phillips, there exist 42 different types of alternating labyrinths with 1 axis and 7 circuits (see: related posts 1). However, he has shown only a selection of 14 of these types on his website. A reader has asked us if we could help him find all 42 types. The answer is yes. All basic information we need is already available in various posts of this blog. First I will recapitulate these basics and later derive the 42 types. 

First, we need some more precise details of the labyrinths shown on Tony’s website and, second, our knowledge of the groups of relative labyrinths. 

As mentioned already earlier (related posts 2), Tony distinguishes between uninteresting, interesting and very interesting labyrinths. Labyrinths in which are attached trivial circuits at the outside or inside (or in greater labyrinths also in between – this, however does not yet apply to labyrinths with 7 circuits) are termed uninteresting. Trivial means attached to one other in the manner of serpentines. Labyrinths in which this is not the case are termed interesting. Particularly, in interesting labyrinths, the pathway does enter the labyrinth on the first circuit and does not reach the center from the innermost circuit either. Very interesting are termed the self-dual among the interesting labyrinths (there are also self-dual uninteresting labyrinths). 

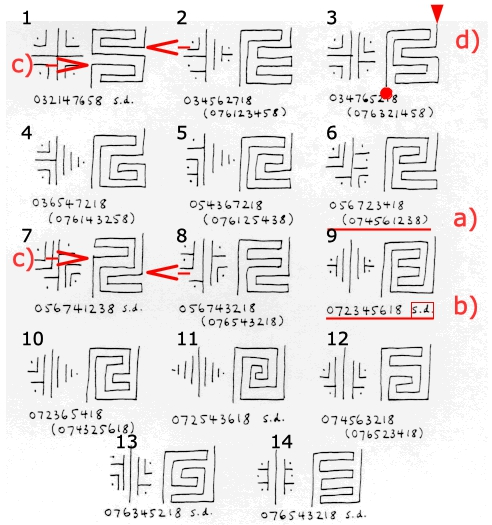
On Tony’s website only 14 patterns and seed patterns of interesting and very interesting labyrinths are depicted, as shown in figure 1 (related posts 3). Of dual labyrinths, only one of the patterns and seed patterns is presented, let us call them base labyrinths. However, the sequence of circuits of the dual is also indicated in parentheses (a). For the very interesting self-dual labyrinths „s.d.“ is indicated in parentheses (b). Thus, the following information is available: six self-dual, very interesting labyrinths and 8 interesting labyrinths to which are also indicated the sequences of circuits of another 8 labyrinths dual to them. Therefore we dispose of information about 22 very interesting and interesting labyrinths and we miss information about 20 labyrinths. 

Figure 1. The 14 Available Patterns and Seed Patterns

Now in addition to dual there are also transpose and complementary labyrinths. Therefore the question is: can we find all missing labyrinths with the transpose and complementary of the 14 available base labyrinths. And the answer is: yes. 

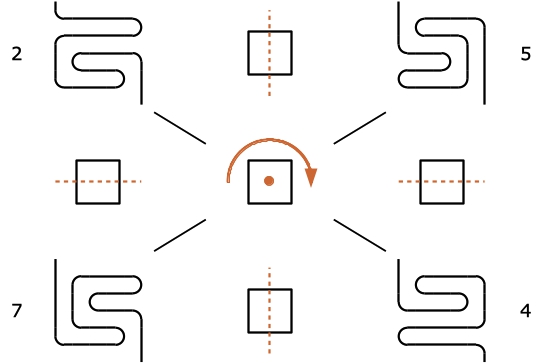
For this, let us remember the actions we use to obtain the dual, transpose and complement of a base labyrinth. These are shown in figure 2 (also this figure comes from an earlier post, see: related posts 4). The dual is obtained by rotating the pattern. The transpose is generate by horizonally mirroring, the complement by vertically mirroring of the pattern, whiles in both cases the connections to the exterior and to the center are flipped. 

Figure 2. Actions

Now, still another distinction is important. The dual of an interesting labyrinth always is also an interesting labyrinth. However, the transpose or the complement of an interesting labyrinth do not necessarily have to be interesting labyrinths too. This is well illustrated in fig. 3 (related posts 5). Labyrinth 5 is an interesting one, similarly the dual of it, labyrinth 7. However, the transpose of labyrinth 5, labyrinth 2, is an uninteresting as the path enters on the first circuit, and the complement of 5, labyrinth 4, is also unintersting, since the path reaches the center from the innermost circuit. 

Figure 3. Illustration

This can be generalized and it means that in a labyrinth with the pathway reaching the center from the first circuit (as in labyrinth 5), the transpose is a labyrinth in which the pathway enters on the first circuit (labyrinth 2), i.e. an uninteresting labyrinth. And also the complement is uninteresting, as the path reaches the center from the innermost circuit (labyrinth 4). And similarly, in an interesting labyrinth with the path entering on the innermost circuit (labyrinth 7), both, the transpose (labyrinth 4) and the complement (labyrinth 2) are uninteresting ones. 

With this in mind we now return tot the 14 images of interesting and very interesting labyrinths on Tony’s website. And here we search all patterns with the pathway entering on the innermost or reaching the center from the outermost circuit. Because the transpose and complementary labyrinths of these labyrinths are uninteresting. Therefore I show in fig. 4 once again fig. 1 and simply number the 14 images from 1 to 14. Here, another addition is needed. Tony draws the patterns such that the entrance lies on top right and the center on bottom left (d).

Figure 4. Numbering

On our search we now find the following labyrinths with their pathway entering on the 7^th or reaching the center from the 1^st circuit: No. 2, No. 3, No. 4, No. 5, No. 6, No. 8, No. 9, No. 10, No. 11, No. 12, No. 13, No. 14. These are all except No. 1 and No. 7 (c). These, No. 1 and No. 7 are very special labyrinths and have been repeatedly mentioned on this blog already. They are complementary to each other. And they are self-dual and thus also transpose to each other. Because in self-dual labyrinths the complements are the same as the transposes (related posts 0). These are the only two labyrinths in which the base / dual are interesting as well as the transpose / complement. Thus, the transposes and complements of the remaining 12 labyrinths from fig. 4 are still missing. 

That is, we search to labyrinths with numbers 2, 3, 4, 5, 6, 8, 10, and 12 two each, to the self-dual labyrinths with numbers 9, 11, 13 und 14 one transpose and complementary labyrinth, thus altogether all 20 missing uninteresting labyrinths. 

Thus, we have the following situation: 14 images, among which 6 very interesting self-dual labyrinths as well as 8 labyrinths and their 8 duals, that is 16 interesting labyirnths, together 22 interesting and very interesting labyrinths. Among these are two very interesting transpose / complementary labyrinths. There remain 4 very interesting labyrinths from which 4 uninteresting labyrinths can be derived and 8 interesting labyrinths from which16 uninteresting labyrinths can be derived. Thus we have shown, that all 42 types of alternating labyrinths with 1 axis and 7 circuits can be derived from the 14 labyrinths depicted in Tony’s figure. In the following posts I will show how to do that. 

Related Posts:

1. The Six Very Interesting Labyrinths with 7 Circuits
2. Un- / interesting Labyrinths
3. Triple Barriers – Patterns for the First and the Last Sector
4. The Related Labyrinths
5. The three Arrangements of the Related Labyrinths

Labyrinth for the New Year 2024

To all our visitors we wish a happy new year 2024!

Labyrinth with 6 Axes and 11 Circuits, self-dual, own design as a Hexagram in the Flower of Life – Style

Related Posts:

• Labyrinth for the New Year 2023
• Labyrinth for the New Year 2022
• Labyrinth for the New Year 2021
• Labyrinth for the New Year 2020
• Labyrinth for the New Year 2019
• Our Best Wishes for 2018
• My Best Wishes for 2017

How to Draw a Man-in-the-Maze Labyrinth /18

Type Gossembrot 51r – Comparing the Courses of the Pathway

I have already described what is special with the Gossembrot 51 r labyrinth in this blog (see: related posts, below). Here I want to compare the courses of the pathway in the original and in the MiM-style. For this, I use figures from the previous post and complement them with a presentation in the MiM-style. The following figures are all composed the same way. On top left the course of the pathway in the original, on top right the course in the MiM-style and below the pattern is shown. 

Figure 1 shows the start of the course of the pathway. The path passes in forward direction until it has circumnavigated the innermost circuit. It becomes already clear here, that in the MiM-style the course is much more complicated than in the original. Compare the situation of the entrance (triangle) at the beginning of the seed pattern and the position of the turning points a, b, and c. And, whereas the 7^th circuit is a closed arc of a circle in the original, in the MiM-style it is transformed to a kind of a aureola. Since this is the innermost circuit there remain only very short pieces of arcs at the outside, whereas the longer pieces of arcs are transfered to the inside where the circuit traverses the side-axes. 

Figure 1. Start of the Pathway

Figure 2 shows the pathway in backward direction until it reaches the second segment of the labyrinth (the segment between the 1. and 2. side-axis). The path passes on circuits 6, 3, and 2 and traverses first the 4. side-axis on circuit 2, then the 3. side-axis on circuit 6, and finally the 2. side-axis on circuit 2 again. 

Figure 2. Backward Movement – Beginning

In fig. 3, the pathway is still on its course in backward direction and first completes the second and then the first segment before turning to circuit 1 at the main axis. It can be seen, that now in the first two segments only circuit 1 is still not covered by the Ariadne’s Thread. Therefore, the further course also becomes better apparent in this figure. From this point, the path goes into a forward movement again. In doing so, it will first traverse the 1. and 2. side-axis and then turn at the 3. side-axis. This piece of the pathway on the 1. circuit is an arc of a circle of 3/5 circumference length. In the MiM-style it transforms to three brackets attached to each other. These are connected by short arcs of circles at the inside where the pathway traverses the axes. 

Figure 3. Backward Movement – End

Figure 4 shows the complete course of the pathway. The path – still in forward direction – has completed the remaining circuits in segments 3, 4, and 5 and then reached the goal. 

Figure 4. The Complete Course of the Pathway

The pattern is the simplest, the Ariadne’s Thread the most complicated presentation of the course of the pathway. The original Ariadne’s Thread lies between. This results form the organization of the seed patterns. In the original, these are aligned axially, i.e along the axes. In the MiM-style they are aligned circularly along the rings. 

Related Posts:

• Sigmund Gossembrot / 2

How to Draw a Man-in-the-Maze Labyrinth / 17

Axes and Circuits in the Type Gossembrot 51r 

Now I want to compare the course of the pathway of the type Gossembrot 51r in original and in the MiM-style. For this, first, some preparatory steps are needed in order to show where the axes and circuits are situated in the MiM-style. 

Figure 1 illustrates the situation of the axes (dashed blue lines). The axes are located in the middle of their corresponding seed patterns. Neighboring seed patterns touch each other with their ends (orange buffers) (see also: related posts, below).

Figure 1. Situation of the Seed Patterns and Axes

Figure 2 shows the entrance to the labyrinth and the center. In the MiM-style it is useful in addition to the number of circuits to term the the outer world with „0“ and the center with „8“, that is with a number one greater than the number of circuits (the labyrinth has 7 circuits). We can see here, that the outer world axially reaches into the figure (0), and the center axially veers to the outside from the seed pattern (8). 

Figure 2. Entrance and Center

Figure 3 indicates the numbering of the circuits. The circuits are formed of a sort of brackets that are composed of an arc of a circle and two axial straights that exit from the circular seed pattern. We can see here in clocwise rotation the seven circuits of the left half of the main axis (1-7), the right half of the first side-axis (7-1), the left half of the first side-axis (1-7), and the right half of the second side-axis (7-1). This numbering could be continued through the whole labyrinth. These brackets connect two adjacent seed patterns each. 

Figure 3. Numbering of the Circuits

In doing so the pathway must traverse the side-axes. How this works in the MiM-style is shown in fig. 4. The circuits 7, 6, and 1 break through the seed pattern’s arcs of circles and continue to the inside of the labyrinth figure, where they traverse the axis as an arc of a circle. 

Figure 4. Traverses of Axes

This provides us with the basis for the presentation of the course of the pathway in the next post.

Related Posts:

• How to Draw a Man-in-the-Maze Labyrinth / 9